Internal Correspondence Analysis

witwit.coa performs an Internal Correspondence Analysis. witwitsepan gives the computation and the barplot of the eigenvalues for each separated analysis in an Internal Correspondence Analysis.

Usage

witwit.coa(dudi, row.blocks, col.blocks, scannf = TRUE, nf = 2)
# S3 method for class 'witwit'
summary(object, ...)
witwitsepan(ww, mfrow = NULL, csub = 2, plot = TRUE)

Arguments

dudi

an object of class coa

row.blocks

a numeric vector indicating the row numbers for each block of rows

col.blocks

a numeric vector indicating the column numbers for each block of columns

scannf

a logical value indicating whether the eigenvalues bar plot should be displayed

nf

if scannf FALSE, an integer indicating the number of kept axes

object

an object of class witwit

...

further arguments passed to or from other methods

ww

an object of class witwit

mfrow

a vector of the form "c(nr,nc)", otherwise computed by a special own function 'n2mfrow'

csub

a character size for the sub-titles, used with par("cex")*csub

plot

if FALSE, numeric results are returned

Value

returns a list of class witwit, coa and dudi (see as.dudi) containing

rbvar

a data frame with the within variances of the rows of the factorial coordinates

lbw

a data frame with the marginal weighting of the row classes

cvar

a data frame with the within variances of the columns of the factorial coordinates

cbw

a data frame with the marginal weighting of the column classes

References

Cazes, P., Chessel, D. and Dolédec, S. (1988) L'analyse des correspondances internes d'un tableau partitionné : son usage en hydrobiologie. Revue de Statistique Appliquée, 36, 39–54.

Author

Daniel Chessel Anne-Béatrice Dufour anne-beatrice.dufour@univ-lyon1.fr Correction by Campo Elías PARDO cepardot@cable.net.co

Examples

data(ardeche)
coa1 <- dudi.coa(ardeche$tab, scann = FALSE, nf = 4)
ww <- witwit.coa(coa1, ardeche$row.blocks, ardeche$col.blocks, scann = FALSE)
ww
#> Duality diagramm
#> class: witwit coa dudi
#> $call: witwit.coa(dudi = coa1, row.blocks = ardeche$row.blocks, col.blocks = ardeche$col.blocks, 
#>     scannf = FALSE)
#> 
#> $nf: 2 axis-components saved
#> $rank: 29
#> eigen values: 0.06858 0.06325 0.04254 0.03566 0.02911 ...
#>   vector length mode    content       
#> 1 $cw    35     numeric column weights
#> 2 $lw    43     numeric row weights   
#> 3 $eig   29     numeric eigen values  
#> 
#>   data.frame nrow ncol content             
#> 1 $tab       43   35   modified array      
#> 2 $li        43   2    row coordinates     
#> 3 $l1        43   2    row normed scores   
#> 4 $co        35   2    column coordinates  
#> 5 $c1        35   2    column normed scores
#> other elements: lbvar lbw cbvar cbw 
summary(ww)
#> Internal correspondence analysis
#> class: witwit coa dudi
#> $call: witwit.coa(dudi = coa1, row.blocks = ardeche$row.blocks, col.blocks = ardeche$col.blocks, 
#>     scannf = FALSE)
#> 2 axis-components saved
#> eigen values: 0.06858 0.06325 0.04254 0.03566 0.02911 ...
#> 
#> Eigen value decomposition among row blocks
#>      Axis1  Axis2  weights
#> Eph  0.0511 0.0563 0.2879 
#> Ple  0.1154 0.0263 0.0653 
#> Col  0.0204 0.0709 0.3703 
#> Tri  0.1403 0.069  0.2766 
#> mean 0.0686 0.0633        
#> 
#>     Axis1 Axis2
#> Eph 214   256  
#> Ple 110   27   
#> Col 110   415  
#> Tri 566   302  
#> sum 1000  1000 
#> 
#> Eigen value decomposition among column blocks
#>       Comp1  Comp2  weights
#> jul82 0.0109 0.0706 0.1859 
#> aug82 0.0413 0.1064 0.1797 
#> nov82 0.017  7e-04  0.1054 
#> feb83 0.1916 0.032  0.1364 
#> apr83 0.1385 0.0613 0.1895 
#> jul83 0.0243 0.0736 0.2031 
#> mean  0.0686 0.0633        
#> 
#>       Comp1 Comp2
#> jul82 29    207  
#> aug82 108   302  
#> nov82 26    1    
#> feb83 381   69   
#> apr83 383   184  
#> jul83 72    236  
#> sum   1000  1000 
#> 

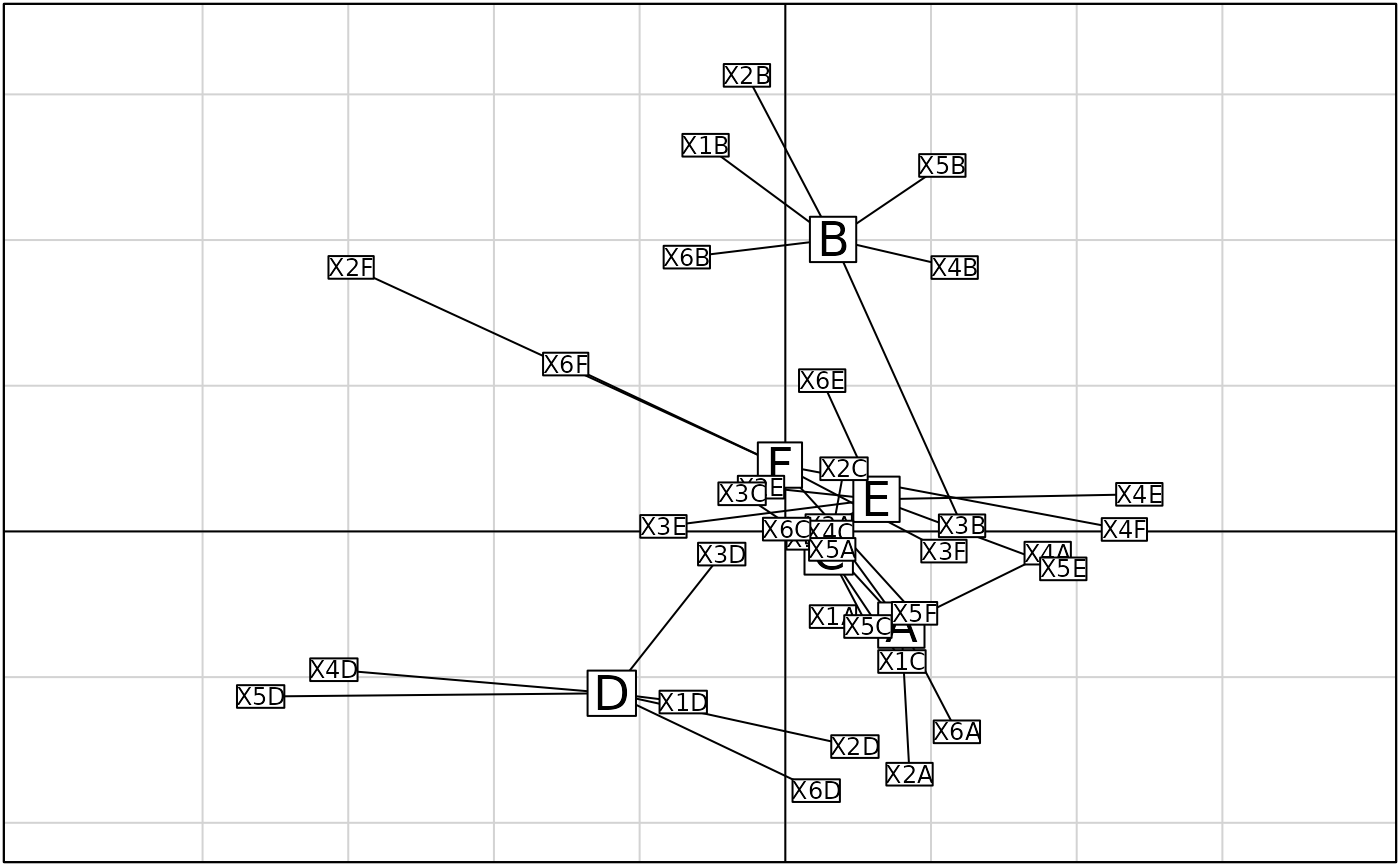
if(adegraphicsLoaded()) {
  g1 <- s.class(ww$co, ardeche$sta.fac, plab.cex = 1.5, ellipseSi = 0, paxes.draw = FALSE, 
    plot = FALSE)
  g2 <- s.label(ww$co, plab.cex = 0.75, plot = FALSE)
  G <- superpose(g1, g2, plot = TRUE)
  
} else {
  s.class(ww$co, ardeche$sta.fac, clab = 1.5, cell = 0, axesell = FALSE)
  s.label(ww$co, add.p = TRUE, clab = 0.75)
}


witwitsepan(ww, c(4, 6))