Correspondence Analysis

performs a correspondence analysis.

Usage

dudi.coa(df, scannf = TRUE, nf = 2)

Arguments

df

a data frame containing positive or null values

scannf

a logical value indicating whether the eigenvalues bar plot should be displayed

nf

if scannf FALSE, an integer indicating the number of kept axes

Value

returns a list of class coa and dudi (see dudi) containing

N

the sum of all the values of the initial table

References

Benzécri, J.P. and Coll. (1973) L'analyse des données. II L'analyse des correspondances, Bordas, Paris. 1–620.

Greenacre, M. J. (1984) Theory and applications of correspondence analysis, Academic Press, London.

Author

Daniel Chessel
Anne-Béatrice Dufour anne-beatrice.dufour@univ-lyon1.fr

Examples

data(rpjdl)
chisq.test(rpjdl$fau)$statistic
#> Warning: Chi-squared approximation may be incorrect
#> X-squared 
#>  7323.597 
rpjdl.coa <- dudi.coa(rpjdl$fau, scannf = FALSE, nf = 4)
sum(rpjdl.coa$eig)*rpjdl.coa$N # the same
#> [1] 7323.597

if(adegraphicsLoaded()) {
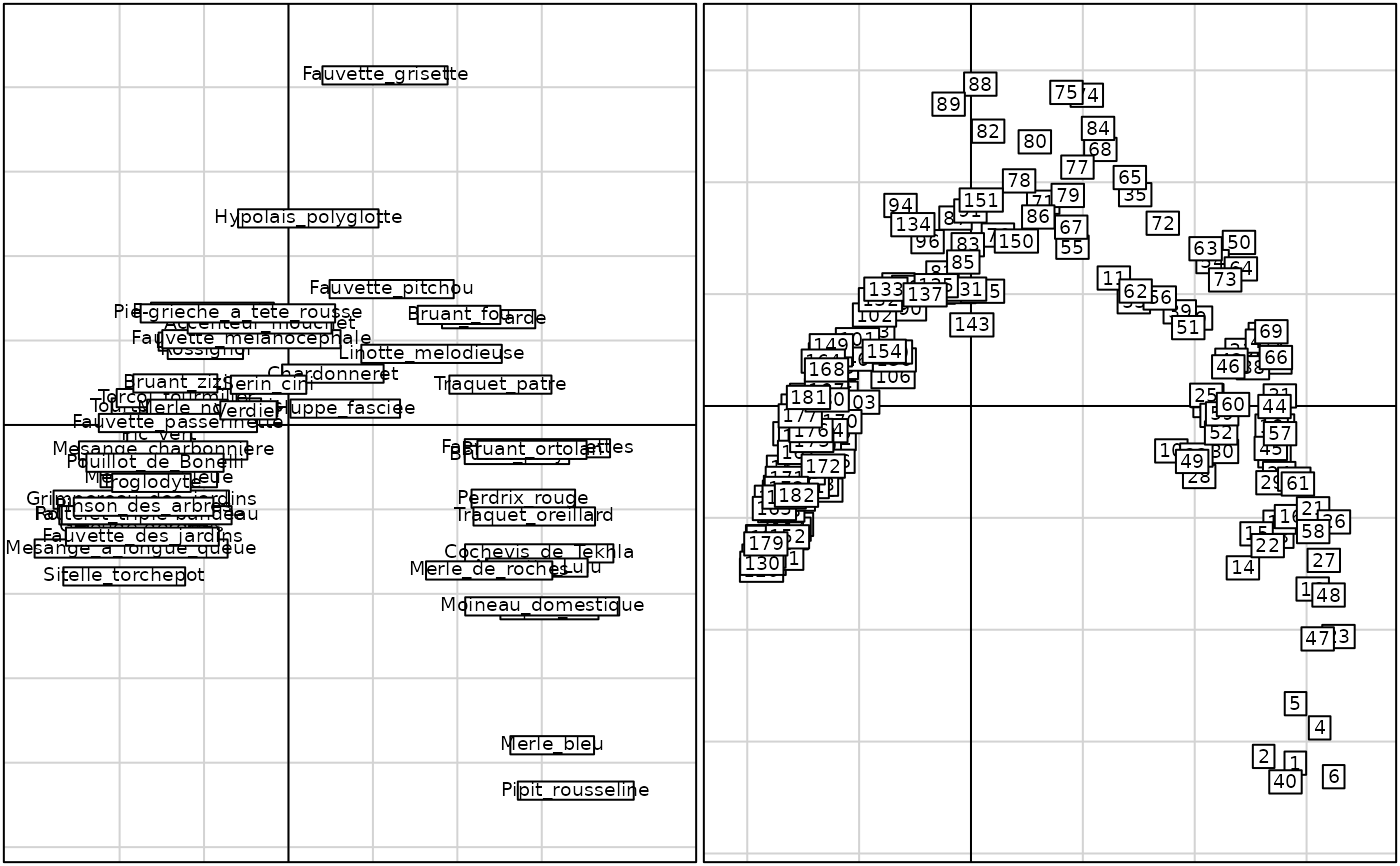
  g1 <- s.label(rpjdl.coa$co, plab.cex = 0.6, lab = rpjdl$frlab, plot = FALSE)
  g2 <- s.label(rpjdl.coa$li, plab.cex = 0.6, plot = FALSE)
  cbindADEg(g1, g2, plot = TRUE)
} else {
  par(mfrow = c(1,2))
  s.label(rpjdl.coa$co, clab = 0.6, lab = rpjdl$frlab)
  s.label(rpjdl.coa$li, clab = 0.6)
  par(mfrow = c(1,1))
}


data(bordeaux)
db <- dudi.coa(bordeaux, scan = FALSE)
db
#> Duality diagramm
#> class: coa dudi
#> $call: dudi.coa(df = bordeaux, scannf = FALSE)
#> 
#> $nf: 2 axis-components saved
#> $rank: 3
#> eigen values: 0.5906 0.1102 0.03109
#>   vector length mode    content       
#> 1 $cw    4      numeric column weights
#> 2 $lw    5      numeric row weights   
#> 3 $eig   3      numeric eigen values  
#> 
#>   data.frame nrow ncol content             
#> 1 $tab       5    4    modified array      
#> 2 $li        5    2    row coordinates     
#> 3 $l1        5    2    row normed scores   
#> 4 $co        4    2    column coordinates  
#> 5 $c1        4    2    column normed scores
#> other elements: N 
score(db)