Skip to contents

Monte-Carlo Test on a Discriminant Analysis (in R).

rtest.discrimin.Rd

Test of the sum of a discriminant analysis eigenvalues (divided by the rank). Non parametric version of the Pillai's test. It authorizes any weighting.

Usage

# S3 method for discrimin
rtest(xtest, nrepet = 99, ...)

Arguments

xtest

an object of class discrimin

nrepet

the number of permutations

...

further arguments passed to or from other methods

Value

returns a list of class rtest

Author

Daniel Chessel

Examples

data(meaudret)
pca1 <- dudi.pca(meaudret$env, scan = FALSE, nf = 3)
rand1 <- rtest(discrimin(pca1, meaudret$design$season, scan = FALSE), 99)
rand1
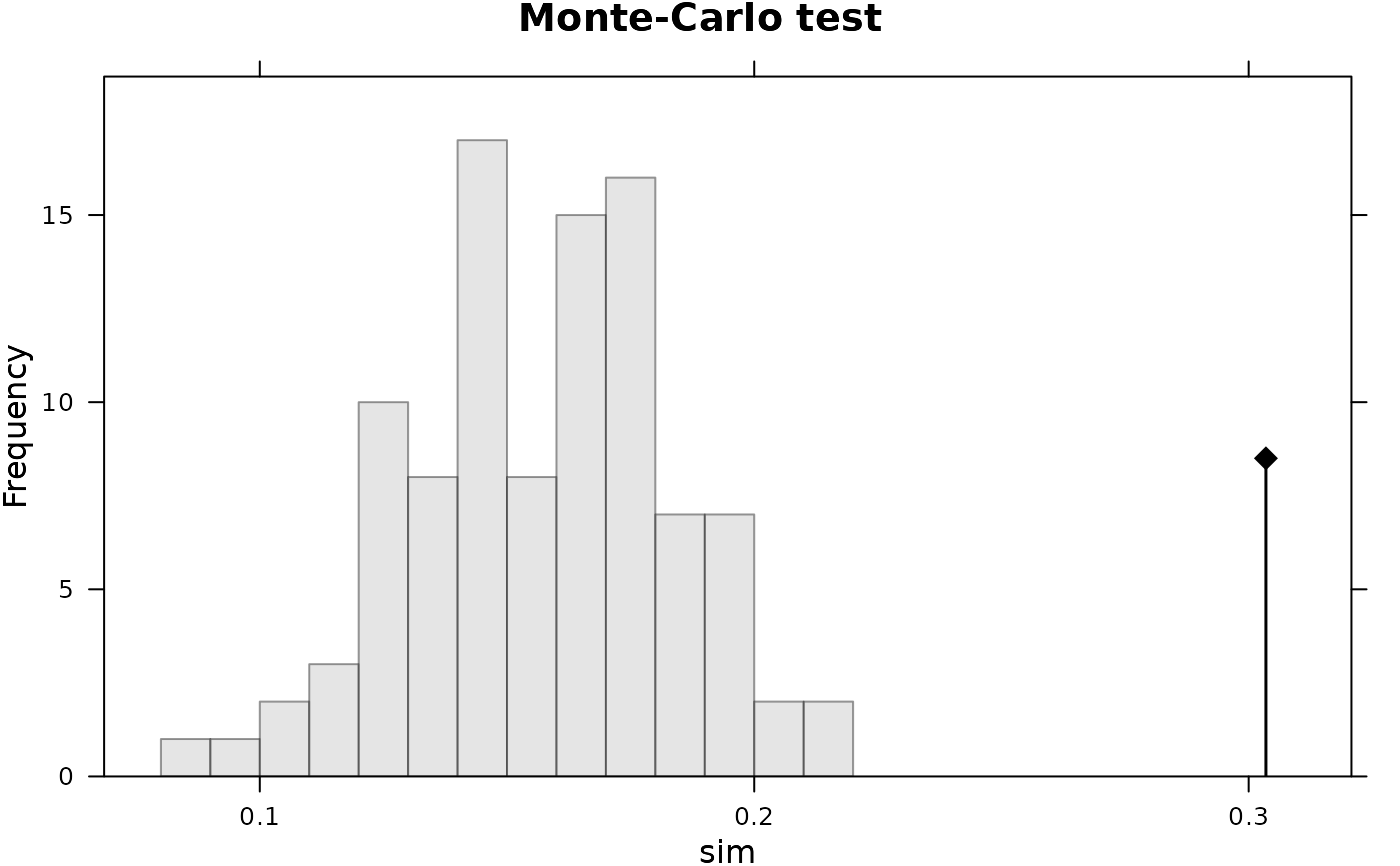
#> Monte-Carlo test
#> Call: rtest.discrimin(xtest = discrimin(pca1, meaudret$design$season, 
#>     scan = FALSE), nrepet = 99)
#> 
#> Observation: 0.3034897 
#> 
#> Based on 99 replicates
#> Simulated p-value: 0.01 
#> Alternative hypothesis: greater 
#> 
#>      Std.Obs  Expectation     Variance 
#> 5.5759183221 0.1571838312 0.0006884794 
#Monte-Carlo test
#Observation: 0.3035 
#Call: as.rtest(sim = sim, obs = obs)
#Based on 999 replicates
#Simulated p-value: 0.001 
plot(rand1, main = "Monte-Carlo test")

summary.manova(manova(as.matrix(meaudret$env)~meaudret$design$season), "Pillai")
#>                        Df Pillai approx F num Df den Df    Pr(>F)    
#> meaudret$design$season  3 2.7314   11.299     27     30 1.636e-09 ***
#> Residuals              16                                            
#> ---
#> Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#                         Df Pillai approx F num Df den Df  Pr(>F)    
# meaudret$design$season  3   2.73    11.30     27     30 1.6e-09 ***
# Residuals         16                                          
# ---
# Signif. codes:  0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1 
# 2.731/9 = 0.3034