Simple Procruste Rotation between two sets of points

performs a simple procruste rotation between two sets of points.

Usage

procuste(dfX, dfY, scale = TRUE, nf = 4, tol = 1e-07) 
# S3 method for class 'procuste'
plot(x, xax = 1, yax = 2, ...)
# S3 method for class 'procuste'
print(x, ...)
# S3 method for class 'procuste'
randtest(xtest, nrepet = 999, ...)

Arguments

dfX, dfY

two data frames with the same rows

scale

a logical value indicating whether a transformation by the Gower's scaling (1971) should be applied

nf

an integer indicating the number of kept axes

tol

a tolerance threshold to test whether the distance matrix is Euclidean : an eigenvalue is considered positive if it is larger than -tol*lambda1 where lambda1 is the largest eigenvalue.

x, xtest

an objet of class procuste

xax

the column number for the x-axis

yax

the column number for the y-axis

nrepet

the number of repetitions to perform the randomization test

...

further arguments passed to or from other methods

Value

returns a list of the class procuste with 9 components

d

a numeric vector of the singular values

rank

an integer indicating the rank of the crossed matrix

nf

an integer indicating the number of kept axes

tabX

a data frame with the array X, possibly scaled

tabY

a data frame with the array Y, possibly scaled

rotX

a data frame with the result of the rotation from array X to array Y

rotY

a data frame with the result of the rotation from array Y to array X

loadX

a data frame with the loadings of array X

loadY

a data frame with the loadings of array Y

scorX

a data frame with the scores of array X

scorY

a data frame with the scores of array Y

call

a call order of the analysis

Author

Daniel Chessel
Anne-Béatrice Dufour anne-beatrice.dufour@univ-lyon1.fr

References

Digby, P. G. N. and Kempton, R. A. (1987) Multivariate Analysis of Ecological Communities. Population and Community Biology Series, Chapman and Hall, London.

Gower, J.C. (1971) Statistical methods of comparing different multivariate analyses of the same data. In Mathematics in the archaeological and historical sciences, Hodson, F.R, Kendall, D.G. & Tautu, P. (Eds.) University Press, Edinburgh, 138–149.

Schönemann, P.H. (1968) On two-sided Procustes problems. Psychometrika, 33, 19–34.

Torre, F. and Chessel, D. (1994) Co-structure de deux tableaux totalement appariés. Revue de Statistique Appliquée, 43, 109–121.

Dray, S., Chessel, D. and Thioulouse, J. (2003) Procustean co-inertia analysis for the linking of multivariate datasets. Ecoscience, 10, 1, 110-119.

Examples

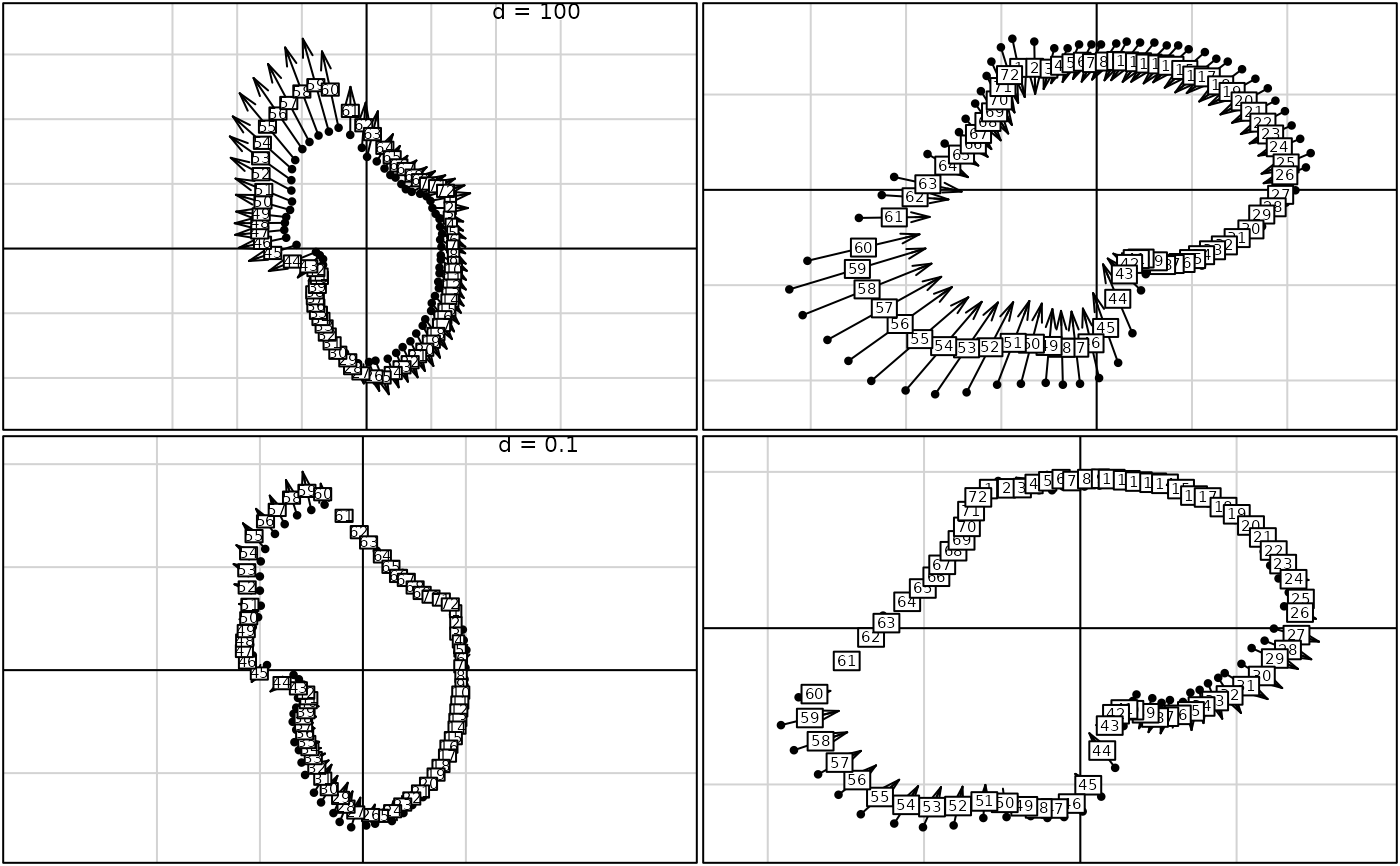
data(macaca)
pro1 <- procuste(macaca$xy1, macaca$xy2, scal = FALSE)
pro2 <- procuste(macaca$xy1, macaca$xy2)
if(adegraphicsLoaded()) {
  g1 <- s.match(pro1$tabX, pro1$rotY, plab.cex = 0.7, plot = FALSE)
  g2 <- s.match(pro1$tabY, pro1$rotX, plab.cex = 0.7, plot = FALSE)
  g3 <- s.match(pro2$tabX, pro2$rotY, plab.cex = 0.7, plot = FALSE)
  g4 <- s.match(pro2$tabY, pro2$rotX, plab.cex = 0.7, plot = FALSE)
  G <- ADEgS(list(g1, g2, g3, g4), layout = c(2, 2))
} else {
  par(mfrow = c(2, 2))
  s.match(pro1$tabX, pro1$rotY, clab = 0.7)
  s.match(pro1$tabY, pro1$rotX, clab = 0.7)
  s.match(pro2$tabX, pro2$rotY, clab = 0.7)
  s.match(pro2$tabY, pro2$rotX, clab = 0.7)
  par(mfrow = c(1,1))
}


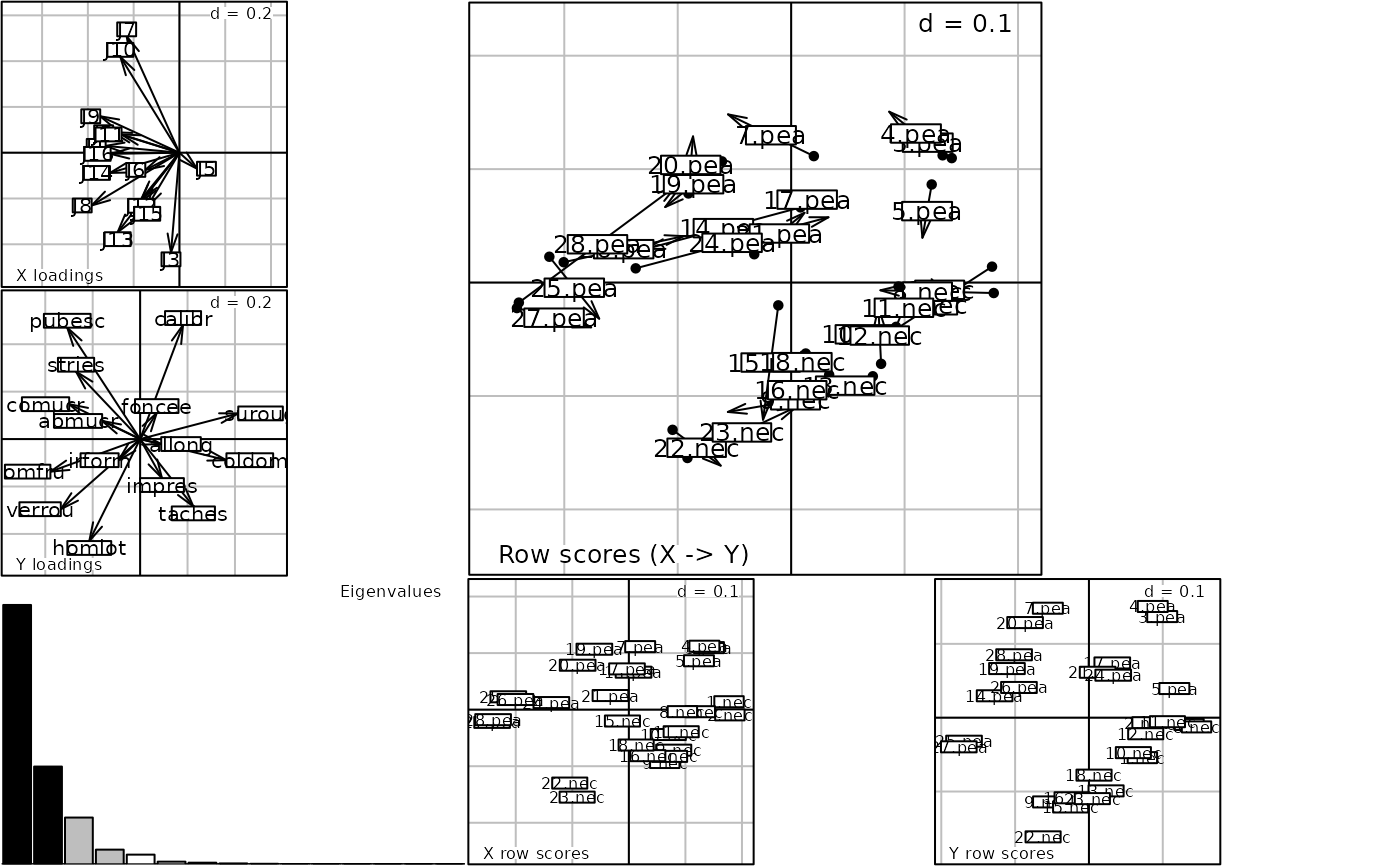
data(doubs)
pca1 <- dudi.pca(doubs$env, scal = TRUE, scann = FALSE)
pca2 <- dudi.pca(doubs$fish, scal = FALSE, scann = FALSE)
pro3 <- procuste(pca1$tab, pca2$tab, nf = 2)
if(adegraphicsLoaded()) {
  g11 <- s.traject(pro3$scorX, plab.cex = 0, plot = FALSE)
  g12 <- s.label(pro3$scorX, plab.cex = 0.8, plot = FALSE)
  g1 <- superpose(g11, g12)
  g21 <- s.traject(pro3$scorY, plab.cex = 0, plot = FALSE)
  g22 <- s.label(pro3$scorY, plab.cex = 0.8, plot = FALSE)
  g2 <- superpose(g21, g22)
  g3 <- s.arrow(pro3$loadX, plab.cex = 0.75, plot = FALSE)
  g4 <- s.arrow(pro3$loadY, plab.cex = 0.75, plot = FALSE)
  G <- ADEgS(list(g1, g2, g3, g4), layout = c(2, 2))

} else {
  par(mfrow = c(2, 2))
  s.traject(pro3$scorX, clab = 0)
  s.label(pro3$scorX, clab = 0.8, add.p = TRUE)
  s.traject(pro3$scorY, clab = 0)
  s.label(pro3$scorY, clab = 0.8, add.p = TRUE)
  s.arrow(pro3$loadX, clab = 0.75)
  s.arrow(pro3$loadY, clab = 0.75)
  par(mfrow = c(1, 1))
}


plot(pro3)
#> Error in s.arrow(dfxy = pro3$loadX, xax = 1, yax = 2, plot = FALSE, storeData = TRUE,     pos = -3, psub = list(text = "X loadings"), plabels = list(        cex = 1.25)): non convenient selection for dfxy (can not be converted to dataframe)
randtest(pro3)
#> Monte-Carlo test
#> Call: procuste.randtest(df1 = df1, df2 = df2, nrepet = nrepet)
#> 
#> Observation: 0.6562 
#> 
#> Based on 999 replicates
#> Simulated p-value: 0.001 
#> Alternative hypothesis: greater 
#> 
#>     Std.Obs Expectation    Variance 
#> 6.920722998 0.341726082 0.002064744 

data(fruits)
plot(procuste(scalewt(fruits$jug), scalewt(fruits$var)))