Computation of Distance Matrices on Quantitative Variables

computes on quantitative variables, some distance matrices as canonical, Joreskog and Mahalanobis.

Usage

dist.quant(df, method = NULL, diag = FALSE, upper = FALSE, 
    tol = 1e-07)

Arguments

df

a data frame containing only quantitative variables

method

an integer between 1 and 3. If NULL the choice is made with a console message. See details

diag

a logical value indicating whether the diagonal of the distance matrix should be printed by `print.dist'

upper

a logical value indicating whether the upper triangle of the distance matrix should be printed by `print.dist'

tol

used in case 3 of method as a tolerance threshold for null eigenvalues

Details

All the distances are of type \(d=\|x-y\|_A = \sqrt{(x-y)^{t}A(x-y)}\)

1 = Canonical

A = Identity

2 = Joreskog

\(A=\frac{1}{diag(cov)}\)

3 = Mahalanobis

A = inv(cov)

Value

an object of class dist

Author

Daniel Chessel
Stéphane Dray stephane.dray@univ-lyon1.fr

Examples

data(ecomor)

if(adegraphicsLoaded()) {
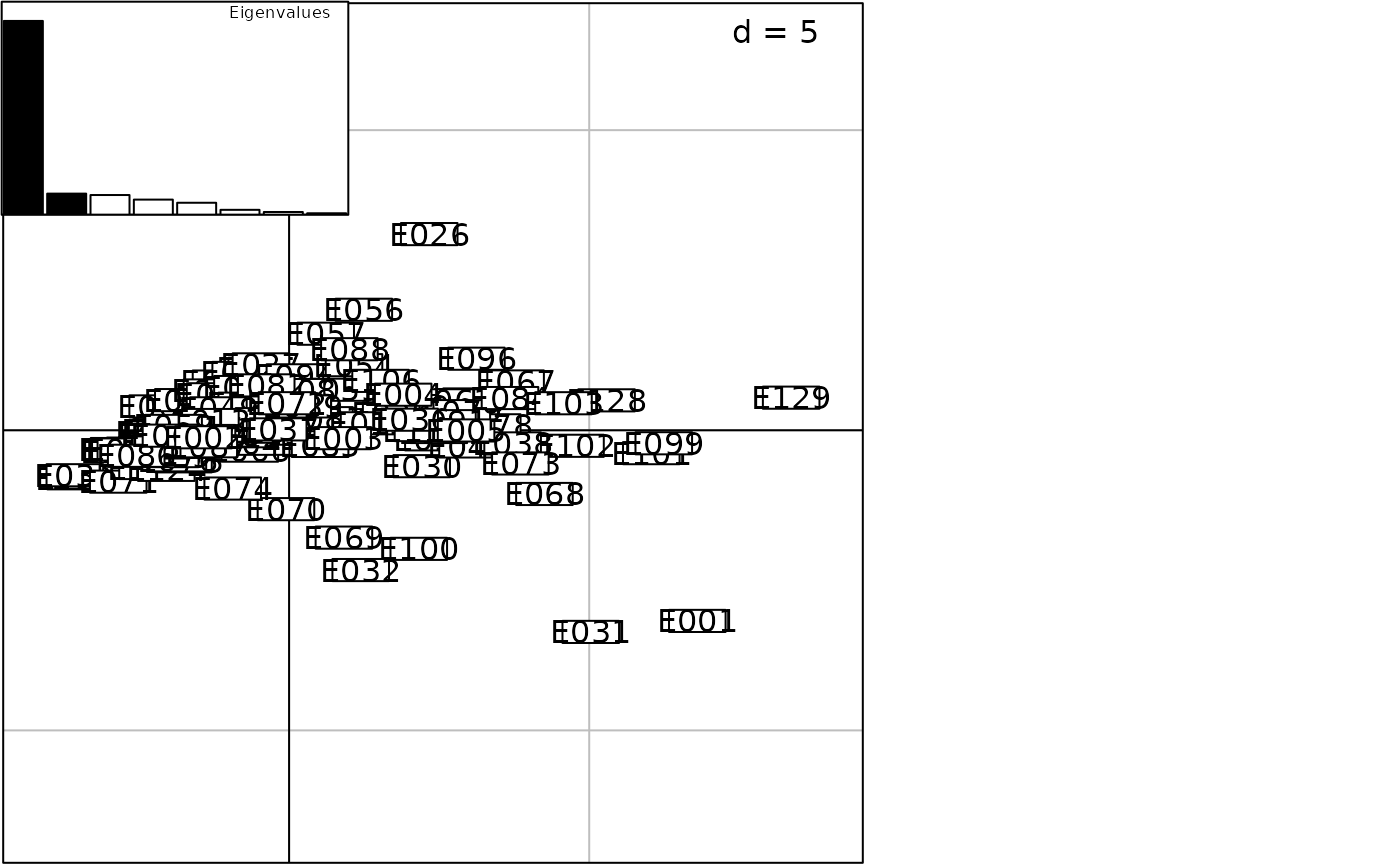
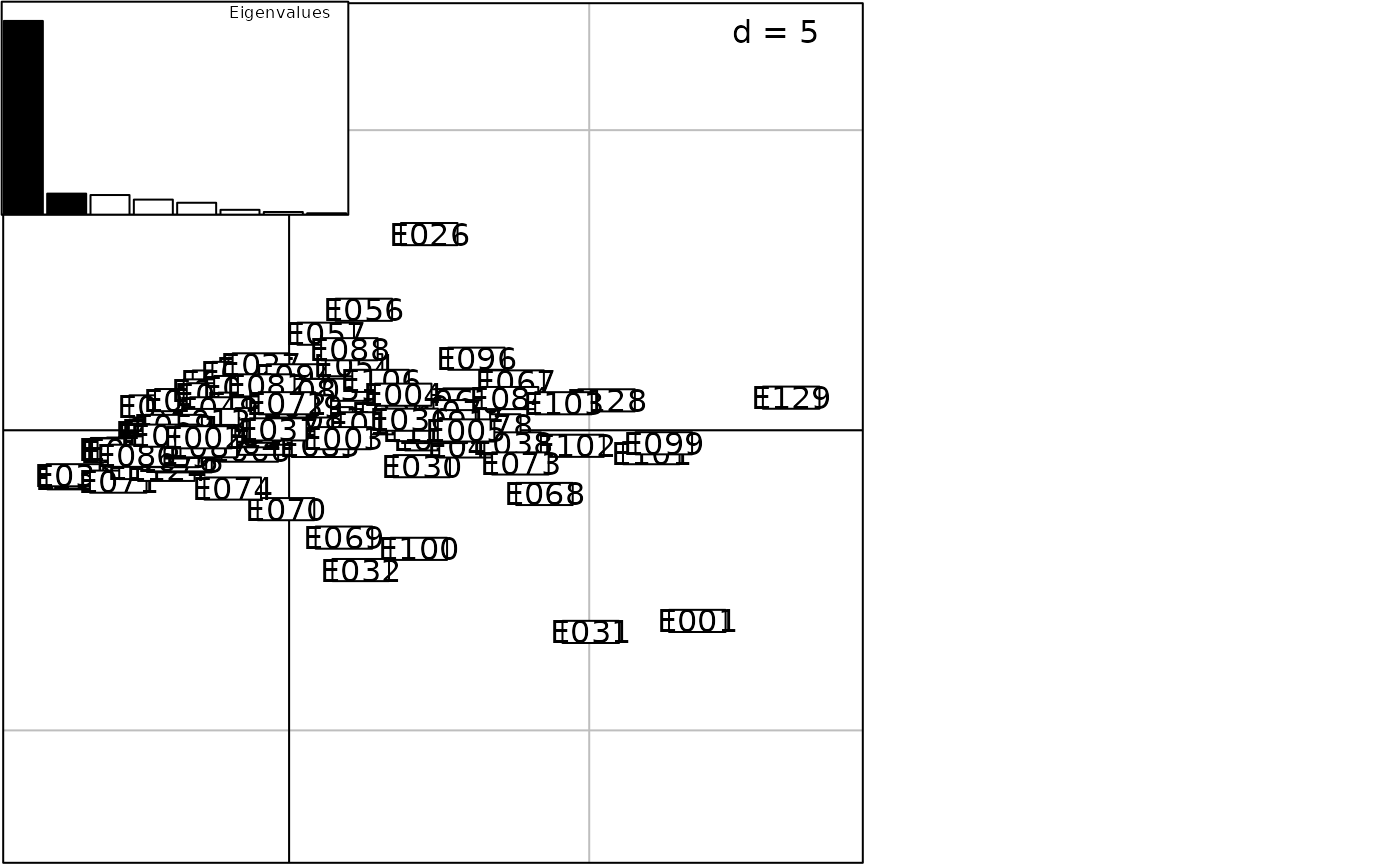
  g1 <- scatter(dudi.pco(dist.quant(ecomor$morpho, 3), scan = FALSE), plot = FALSE)
  g2 <- scatter(dudi.pco(dist.quant(ecomor$morpho, 2), scan = FALSE), plot = FALSE)
  g3 <- scatter(dudi.pco(dist(scalewt(ecomor$morpho)), scan = FALSE), plot = FALSE)
  g4 <- scatter(dudi.pco(dist.quant(ecomor$morpho, 1), scan = FALSE), plot = FALSE)
  G <- ADEgS(list(g1, g2, g3, g4), layout = c(2, 2))
  
} else {
  par(mfrow = c(2, 2))
  scatter(dudi.pco(dist.quant(ecomor$morpho, 3), scan = FALSE))
  scatter(dudi.pco(dist.quant(ecomor$morpho, 2), scan = FALSE))
  scatter(dudi.pco(dist(scalewt(ecomor$morpho)), scan = FALSE))
  scatter(dudi.pco(dist.quant(ecomor$morpho, 1), scan = FALSE))
  par(mfrow = c(1, 1))
}