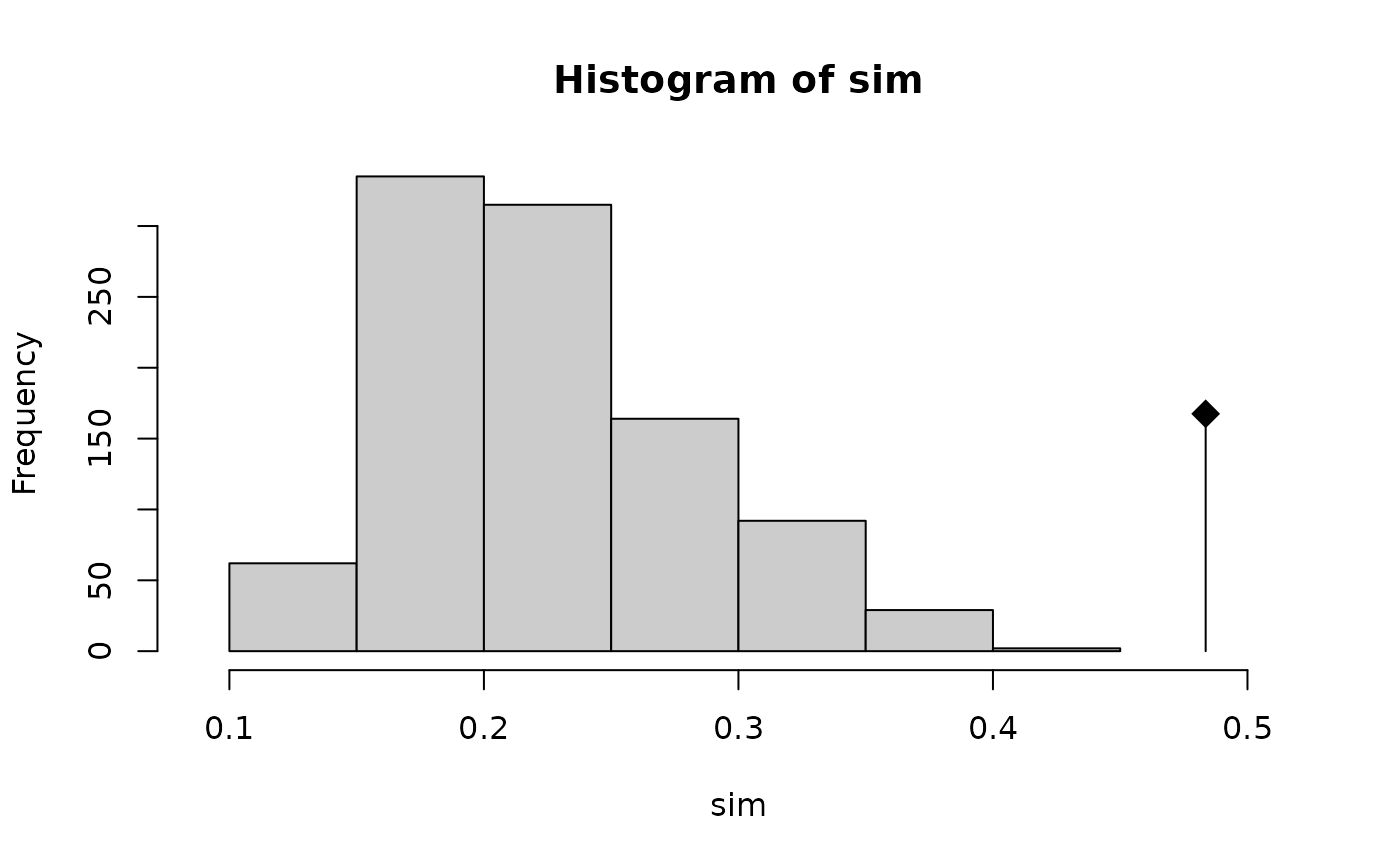
Monte-Carlo Test on the sum of eigenvalues of a within-class co-inertia analysis (in C++ with Rcpp).

performs a Monte-Carlo Test on the sum of eigenvalues of a within-class co-inertia analysis.

Usage

RVintra.randtest(df1, df2, fac, nrepet = 999, ...)

Arguments

df1, df2: two data frames with the same rows
fac: the factor defining classes
nrepet: the number of permutations
...: further arguments passed to or from other methods

Value

returns a list of class 'randtest'

References

Heo, M. & Gabriel, K.R. (1997) A permutation test of association between configurations by means of the RV coefficient. Communications in Statistics - Simulation and Computation, 27, 843-856.

Author

Daniel Chessel and Jean Thioulouse

Examples

data(meaudret)
pca1 <- dudi.pca(meaudret$env, scan = FALSE, nf = 4)
pca2 <- dudi.pca(meaudret$spe, scal = FALSE, scan = FALSE, nf = 4)
wit1 <- wca(pca1, meaudret$design$season, scan = FALSE, nf = 2)
wit2 <- wca(pca2, meaudret$design$season, scan = FALSE, nf = 2)
coiw <- coinertia(wit1, wit2, scann = FALSE)
rv1 <- RVintra.randtest(pca1$tab, pca2$tab, meaudret$design$season, nrep=999)
rv1
#> Monte-Carlo test
#> Call: RVintra.randtest(df1 = pca1$tab, df2 = pca2$tab, fac = meaudret$design$season, 
#>     nrepet = 999)
#> 
#> Observation: 0.4835754 
#> 
#> Based on 999 replicates
#> Simulated p-value: 0.001 
#> Alternative hypothesis: greater 
#> 
#>     Std.Obs Expectation    Variance 
#> 4.521164133 0.224236399 0.003290297 
plot(rv1)