Distance Matrices

This data set gives 3 matrices about geographical, genetic and anthropometric distances.

Usage

data(yanomama)

Format

yanomama is a list of 3 components:

geo

is a matrix of 19-19 geographical distances

gen

is a matrix of 19-19 SFA (genetic) distances

ant

is a matrix of 19-19 anthropometric distances

Source

Spielman, R.S. (1973) Differences among Yanomama Indian villages: do the patterns of allele frequencies, anthropometrics and map locations correspond? American Journal of Physical Anthropology, 39, 461–480.

References

Table 7.2 Distance matrices for 19 villages of Yanomama Indians. All distances are as given by Spielman (1973), multiplied by 100 for convenience in: Manly, B.F.J. (1991) Randomization and Monte Carlo methods in biology Chapman and Hall, London, 1–281.

Examples

    data(yanomama)
    gen <- quasieuclid(as.dist(yanomama$gen)) # depends of mva
    ant <- quasieuclid(as.dist(yanomama$ant)) # depends of mva
    par(mfrow = c(2,2))
    plot(gen, ant)
    t1 <- mantel.randtest(gen, ant, 99);
    plot(t1, main = "gen-ant-mantel") ; print(t1)
#> Monte-Carlo test
#> Call: mantel.randtest(m1 = gen, m2 = ant, nrepet = 99)
#> 
#> Observation: 0.2999879 
#> 
#> Based on 99 replicates
#> Simulated p-value: 0.04 
#> Alternative hypothesis: greater 
#> 
#>      Std.Obs  Expectation     Variance 
#>  1.827914868 -0.008470837  0.028476213 
    t1 <- procuste.rtest(pcoscaled(gen), pcoscaled(ant), 99)
    plot(t1, main = "gen-ant-procuste") ; print(t1)
#> Monte-Carlo test
#> Call: procuste.rtest(df1 = pcoscaled(gen), df2 = pcoscaled(ant), nrepet = 99)
#> 
#> Observation: 0.6819023 
#> 
#> Based on 99 replicates
#> Simulated p-value: 0.01 
#> Alternative hypothesis: greater 
#> 
#>     Std.Obs Expectation    Variance 
#> 3.396865708 0.541544013 0.001707338 
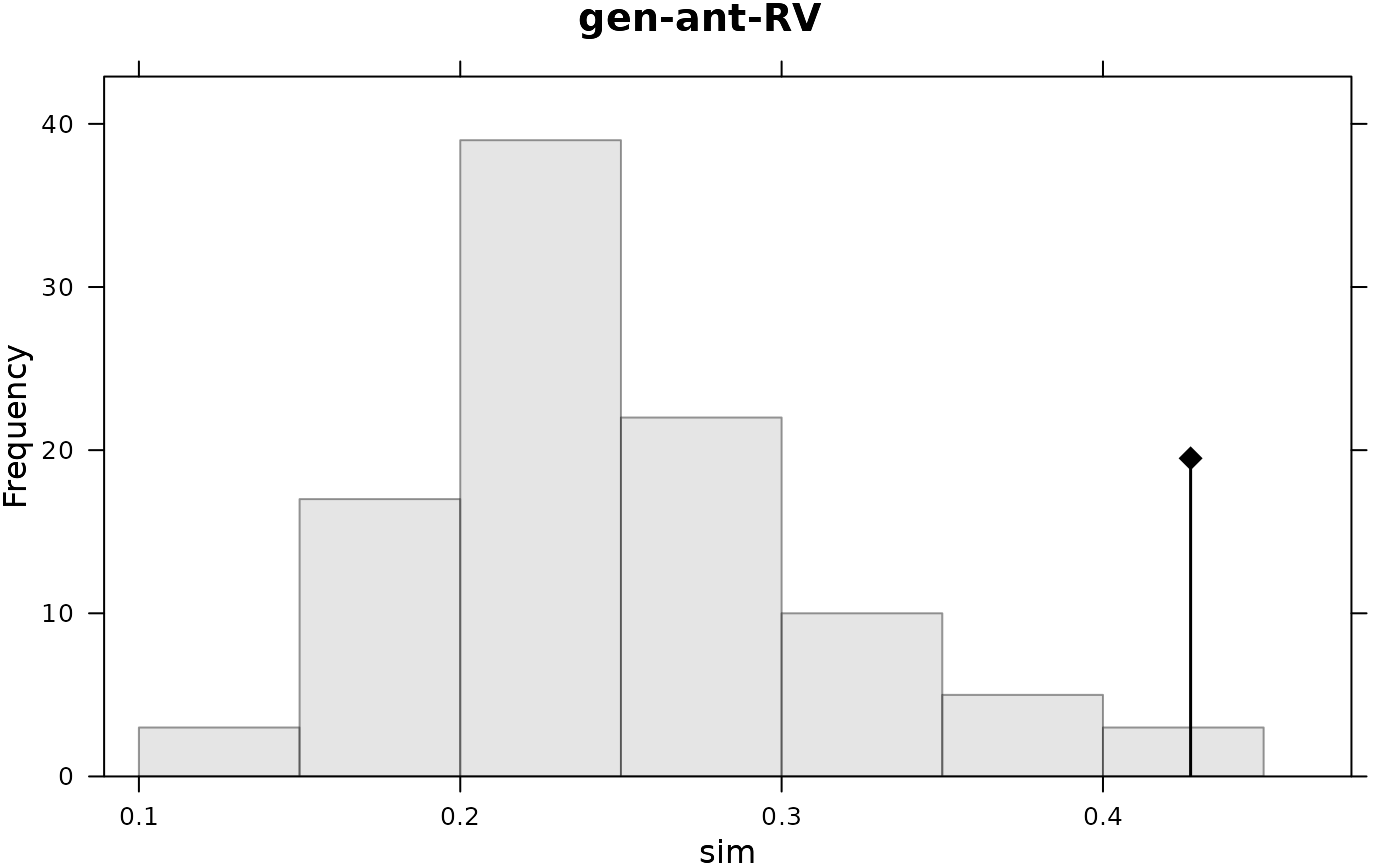
    t1 <- RV.rtest(pcoscaled(gen), pcoscaled(ant), 99)
    plot(t1, main = "gen-ant-RV") ; print(t1)
#> Monte-Carlo test
#> Call: RV.rtest(df1 = pcoscaled(gen), df2 = pcoscaled(ant), nrepet = 99)
#> 
#> Observation: 0.4272698 
#> 
#> Based on 99 replicates
#> Simulated p-value: 0.03 
#> Alternative hypothesis: greater 
#> 
#>     Std.Obs Expectation    Variance 
#> 2.751980726 0.253456163 0.003989118