Neighbourhood Graphs — neig • ade4

neig creates objects of class neig with :
a list of edges
a binary square matrix
a list of vectors of neighbours
an integer (linear and circular graphs)
a data frame of polygons (area)

scores.neig returns the eigenvectors of neighbouring,
orthonormalized scores (null average, unit variance 1/n and null covariances) of maximal autocorrelation.

nb2neig returns an object of class neig using an object of class nb in the library 'spdep'

neig2nb returns an object of class nb using an object of class neig

neig2mat returns the incidence matrix between edges (1 = neighbour ; 0 = no neighbour)

neig.util.GtoL and neig.util.LtoG are utilities.

Usage

neig(list = NULL, mat01 = NULL, edges = NULL,
    n.line = NULL, n.circle = NULL, area = NULL)

scores.neig  (obj) 
# S3 method for class 'neig'
print(x, ...) 
# S3 method for class 'neig'
summary(object, ...)
nb2neig (nb)
neig2nb (neig)
neig2mat (neig)

Arguments

list: a list which each component gives the number of neighbours
mat01: a symmetric square matrix of 0-1 values
edges: a matrix of 2 columns with integer values giving a list of edges
n.line: the number of points for a linear plot
n.circle: the number of points for a circular plot
area: a data frame containing a polygon set (see area.plot)
nb: an object of class 'nb'
neig, x, obj, object: an object of class 'neig'
...: further arguments passed to or from other methods

References

Thioulouse, J., D. Chessel, and S. Champely. 1995. Multivariate analysis of spatial patterns: a unified approach to local and global structures. Environmental and Ecological Statistics, 2, 1–14.

Author

Daniel Chessel

Examples

if(!adegraphicsLoaded()) {
  
  if(requireNamespace("deldir", quietly = TRUE)) {
  
    data(mafragh)
    par(mfrow = c(2, 1))
    provi <- deldir::deldir(mafragh$xy)
    provi.neig <- neig(edges = as.matrix(provi$delsgs[, 5:6]))
    
    s.label(mafragh$xy, neig = provi.neig, inc = FALSE, 
      addax = FALSE, clab = 0, cnei = 2)
    dist <- apply(provi.neig, 1, function(x) 
      sqrt(sum((mafragh$xy[x[1], ] - mafragh$xy[x[2], ]) ^ 2)))
    #hist(dist, nclass = 50)
    mafragh.neig <- neig(edges = provi.neig[dist < 50, ])
    s.label(mafragh$xy, neig = mafragh.neig, inc = FALSE, 
      addax = FALSE, clab = 0, cnei = 2)
    par(mfrow = c(1, 1))
    
    data(irishdata)
    irish.neig <- neig(area = irishdata$area)
    summary(irish.neig)
    print(irish.neig)
    s.label(irishdata$xy, neig = irish.neig, cneig = 3,
      area = irishdata$area, clab = 0.8, inc = FALSE)
    
    irish.scores <- scores.neig(irish.neig)
    par(mfrow = c(2, 3))
    for(i in 1:6)
      s.value(irishdata$xy, irish.scores[, i], inc = FALSE, grid = FALSE, addax = FALSE,
        neig = irish.neig, csi = 2, cleg = 0, sub = paste("Eigenvector ",i), csub = 2)
    par(mfrow = c(1, 1))
    
    a.neig <- neig(n.circle = 16)
    a.scores <- scores.neig(a.neig)
    xy <- cbind.data.frame(cos((1:16) * pi / 8), sin((1:16) * pi / 8))
    par(mfrow = c(4, 4))
    for(i in 1:15)
      s.value(xy, a.scores[, i], neig = a.neig, csi = 3, cleg = 0)
    par(mfrow = c(1, 1))
    
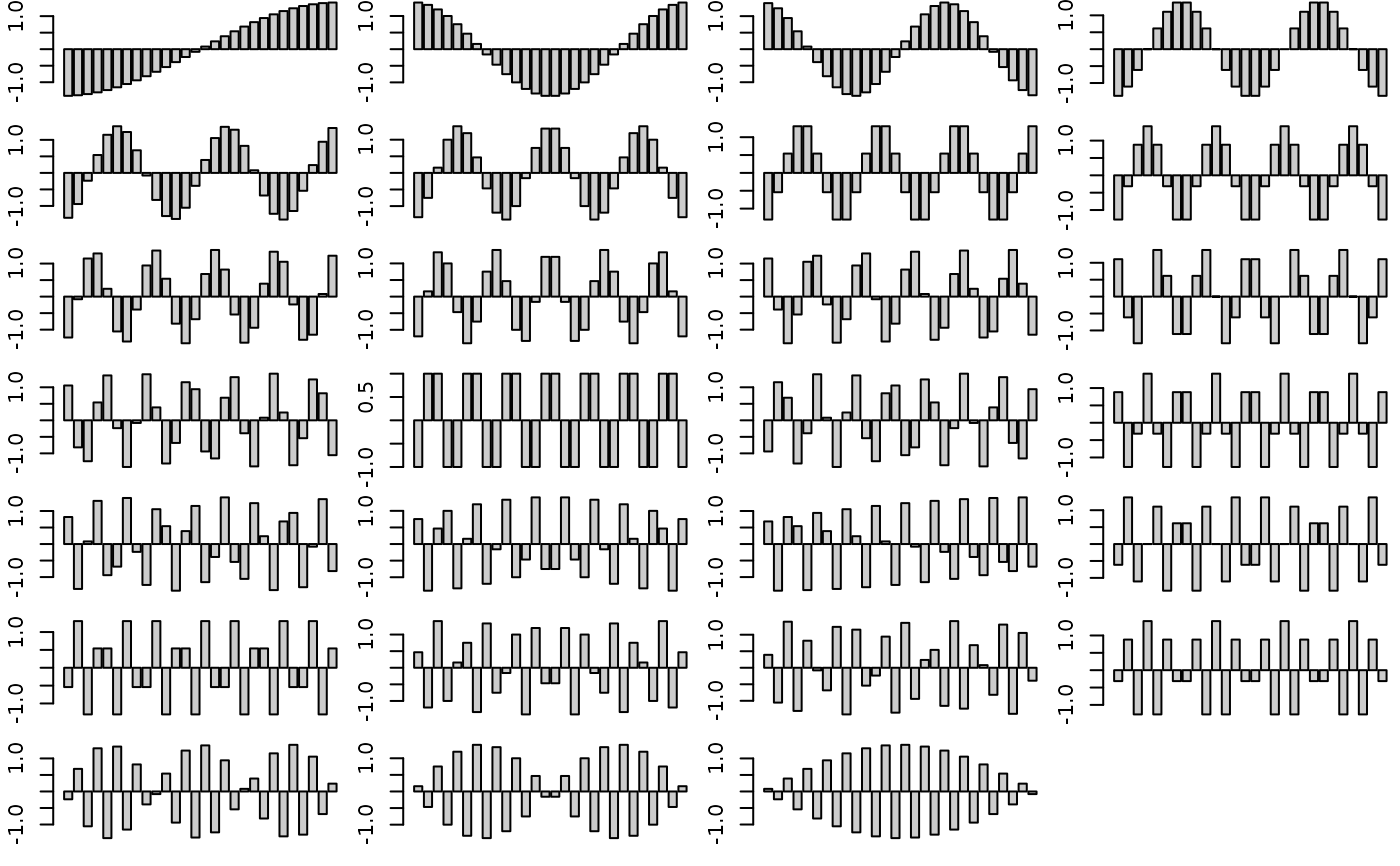
    a.neig <- neig(n.line = 28)
    a.scores <- scores.neig(a.neig)
    par(mfrow = c(7, 4))
    par(mar = c(1.1, 2.1, 0.1, 0.1))
    for(i in 1:27)
      barplot(a.scores[, i], col = grey(0.8))
    par(mfrow = c(1, 1))
  }

  if(requireNamespace("spdep", quietly = TRUE)) {
    
    data(mafragh)
    maf.rel <- spdep::relativeneigh(as.matrix(mafragh$xy))
    maf.rel <- spdep::graph2nb(maf.rel)
    s.label(mafragh$xy, neig = neig(list = maf.rel), inc = FALSE,
      clab = 0, addax = FALSE, cne = 1, cpo = 2)
    
    par(mfrow = c(2, 2))
    w <- matrix(runif(100), 50, 2)
    x.gab <- spdep::gabrielneigh(w)
    x.gab <- spdep::graph2nb(x.gab)
    s.label(data.frame(w), neig = neig(list = x.gab), inc = FALSE,
      clab = 0, addax = FALSE, cne = 1, cpo = 2, sub = "relative")
    x.rel <- spdep::relativeneigh(w)
    x.rel <- spdep::graph2nb(x.rel)
    s.label(data.frame(w), neig = neig(list = x.rel), inc = FALSE,
      clab = 0, addax = FALSE, cne = 1, cpo = 2, sub = "Gabriel")
    k1 <- spdep::knn2nb(spdep::knearneigh(w))
    s.label(data.frame(w), neig = neig(list = k1), inc = FALSE,
      clab = 0, addax = FALSE, cne = 1, cpo = 2, sub = "k nearest neighbours")
    
    all.linked <- max(unlist(spdep::nbdists(k1, w)))
    z <- spdep::dnearneigh(w, 0, all.linked)
    s.label(data.frame(w), neig = neig(list = z), inc = FALSE, clab = 0, 
      addax = FALSE, cne = 1, cpo = 2, sub = "Neighbourhood contiguity by distance")
    par(mfrow = c(1, 1))
  }
  
}

#> Neigbourhood undirected graph
#> Vertices: 25 
#> Degrees: 5 5 4 4 1 5 3 6 5 5 5 4 4 2 3 7 3 7 7 3 8 4 6 4 4 
#> Edges (pairs of vertices): 57 
#> S01 .
#> S02 ..
#> S03 ...
#> S04 ....
#> S05 .....
#> S06 ..1...
#> S07 ..11...
#> S08 1.......
#> S09 1........
#> S10 1......11.
#> S11 .1..1......
#> S12 ..11..1.....
#> S13 .1........1..
#> S14 ..............
#> S15 .....1.........
#> S16 .1.....1.....1..
#> S17 .1...........1.1.
#> S18 .....1.1.1.....1..
#> S19 .....1....1.1.1..1.
#> S20 ..........1...1...1.
#> S21 ..11.1..11.1.....1...
#> S22 ...1....1...........1.
#> S23 .1.....1....1..1.11....
#> S24 1.......1............1..
#> S25 1......1.......1.......1.





#> Warning: neighbour object has 14 sub-graphs