Function to compute multivariate empirical variogram

Compute a multivariate empirical variogram. It is strictly equivalent to summing univariate variograms

variogmultiv(Y, xy, dmin = 0, dmax = max(dist(xy)), nclass = 20)

Arguments

Y

A matrix with numeric data

xy

A matrix with coordinates of samples

dmin

The minimum distance value at which the variogram is computed (i.e. lower bound of the first class)

dmax

The maximum distance value at which the variogram is computed (i.e. higher bound of the last class)

nclass

Number of classes of distances

Value

A list:

d

Distances (i.e. centers of distance classes).

var

Empirical semi-variances.

n.w

Number of connections between samples for a given distance.

n.c

Number of samples used for the computation of the variogram.

dclass

Character vector with the names of the distance classes.

References

Wagner H. H. (2003) Spatial covariance in plant communities: integrating ordination, geostatistics, and variance testing. Ecology, 84, 1045–1057

Author

Stéphane Dray stephane.dray@univ-lyon1.fr

Examples

if(require(ade4)){
data(oribatid)
# Hellinger transformation
fau <- sqrt(oribatid$fau / outer(apply(oribatid$fau, 1, sum), rep(1, ncol(oribatid$fau)), "*"))
# Removing linear effect
faudt <- resid(lm(as.matrix(fau) ~ as.matrix(oribatid$xy))) 
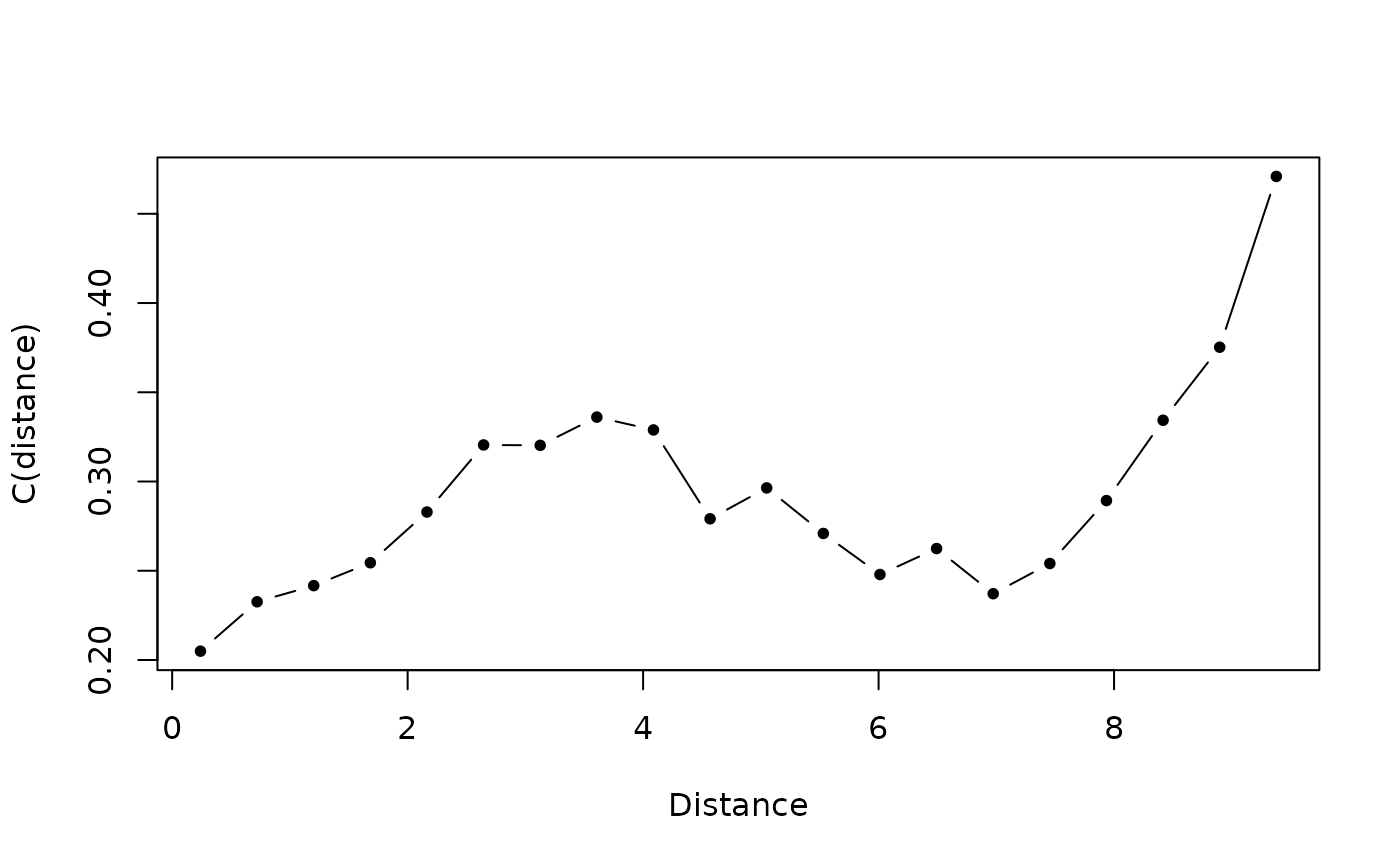
mvspec <- variogmultiv(faudt, oribatid$xy, nclass = 20)
mvspec
plot(mvspec$d, mvspec$var,type = 'b', pch = 20, xlab = "Distance", ylab = "C(distance)")
}