Perform a test of the shared space-environment fraction of a variation partitioning using torus-translation (TT) or Moran Spectral Randomisation (MSR)

The function uses two different spatially-constrained null models to test the shared space-environment fraction (SSEF, or fraction [b]) of a variation partitioning of two explanatory components.

envspace.test(
  spe,
  env,
  coord,
  MEM.spe,
  listw.env,
  MEM.autocor = c("positive", "negative", "all"),
  regular = FALSE,
  nperm = 999,
  MSR.method = "singleton",
  alpha = 0.05
)

Arguments

spe: Vector, matrix, or dataframe of response variable(s) (e.g. species abundances)
env: Vector, matrix, or dataframe of environmental variables (rows = sites, columns = variables)
coord: Matrix or dataframe of spatial coordinates of the sampled sites
MEM.spe: Matrix or dataframe of spatial predictors (MEM variables) selected for spe
listw.env: An object of class listw (spatial weights) created by the functions of the spdep package or returned by listw.candidates
MEM.autocor: A string indicating the type of spatial structure of interest for env ("positive", "negative", or "all", for positive, negative, or both types of spatial autocorrelations, respectively); Default is "positive"
regular: Logical argument indicating whether a torus-translation test will be performed, in addition to the MSR. Set to TRUE only if the sampling design is regular (same number of sites on each line, same number of sites on each column). Set to FALSE otherwise; Default is FALSE
nperm: Number of permutations performed; Default is 999
MSR.method: Algorithm of msr to be used to perform the MSR. The three available procedures are "singleton" (default), "pair", and "triplet" (see msr for details)
alpha: Threshold value of null hypothesis rejection for the test of a spatial structure in the environment, and for the shared environment-space fraction of the variation partitioning; Default is 0.05

Value

If the condition of env being spatially structured is fulfilled, the test is performed and the function returns an object of class randtest containing the results of the test.

Details

The function tests the SSEF (also known as fraction [b]) of a variation partitioning of a response variable or matrix (y) between an environmental and a spatial component (env, and MEM.spe, respectively). The SSEF is the explained variation of y shared by env and MEM.spe. The adjusted R-squared (Peres-Neto et al. 2006; R2adj) of the SSEF is not an actual R2, as it is computed by subtracting the adjusted R2adj of other fractions and therefore has zero degree of freedom (Legendre and Legendre 2012). The SSEF can therefore not be computed in the classical way (residuals permutation; Anderson and Legendre 1999, Legendre and Legendre 2012).

The function envspace.test provides two ways of testing this fraction, that is, spatially-constrained null models based either on a torus-translation test (TT) (for regular sampling designs only), or on Moran spectral randomizations (MSR) (for any type of sampling design). The test of the SSEF should only be performed if both the global models of y against all the environmental variables and against all spatial variables are significant (see Bauman et al. 2018c). The function first checks whether the environment displays significant spatial structures, and then proceeds to the test of the SSEF if this condition is fulfilled (details in Bauman et al. 2018c).

spe can be a vector or a multicolumn matrix or dataframe (multivariate response data). If multivariate, it is greatly advised to transform spe prior to performing the variation partitioning and testing the SSEF (e.g., Hellinger transformation; see Legendre and Gallagher 2001).

MEM.spe is a set of spatial predictors (MEM variables). It is recommended to be a well-defined subset of MEM variables selected among the complete set generated from the spatial weighting matrix (SWM) (see review about spatial eigenvector selection in Bauman et al. 2018a). Optimising the selection of a subset of forward-selected MEM variables among a set of candidate SWMs has been shown to increase statistical power as well as R2-estimation accuracy (Bauman et al. 2018b). To do so, MEM.spe can be generated using listw.candidates followed by listw.select. If a SWM has already been selected in another way, then mem.select can be used to generate the MEM variables and to select an optimal subset among them, which can then be used as MEM.spe in envspace.test (see Details of function mem.select). listw.env corresponds to the SWM that will be used to test for a spatial structure in env, and to build the MEM variables for the MSR test. The choice of the SWM for env can also be optimised with listw.select. The SWMs selected for spe and env should be optimised separately to best model the spatial structure of both spe and env (see example).

To verify that env displays a significant spatial pattern, prior to performing the test of the SSEF, a residuals permutation test is performed on the global set of MEM variables (generated internally from listw.env) associated to the type of spatial structure of interest (see argument MEM.autocor). This test is performed with mem.select. The choice of MEM.autocor should be made according to the MEM.autocor argument used to build MEM.spe.

env is a dataset of environmental variables chosen by the user. We recommend dealing with collinearity issues prior to performing the variation partitioning and the test of the SSEF (see Dormann et al. 2013 for a review of methods to cope with collinearity).

regular is a logical argument indicating whether a TT test should be performed instead of the MSR to test the SSEF. Since the TT can only be performed on regular sampling designs, regular should only be set to TRUE if the sampling design is either a transect, or a grid displaying the same number of sites for all lines and columns (although the number of sites per column can differ from the number of sites per line).

listw.env is the SWM used by the MSR to generate spatially-constrained null environmental variables. It should ideally be a SWM optimised on the basis of env using the function listw.select, with the argument method = "global" (see Details of function mem.select for an explanation). This will allow detecting the spatial structures of env as accurately as possible, hence allowing MSR to generate null environmental variables as spatially faithful to the original ones. It is also on the basis of listw.env that MEM variables will be generated to test whether env is spatially structured (i.e. global test) prior to perform the test of the SSEF.

It is worth mentioning that, although a significant SSEF may provide evidence of an induced spatial dependence (Bauman et al. 2018c), a non-significant SSEF only indicates that no induced spatial dependence could be detected in relation with the chosen environmental variables. This does not exclude that this effect may exist with respect to some unmeasured variables.

References

Anderson M. and Legendre P. (1999) An empirical comparison of permutation methods for tests of partial regression coefficients in a linear model. Journal of Statistical Computation and Simulation, 62(3), 271–303

Bauman D., Drouet T., Dray S. and Vleminckx J. (2018a) Disentangling good from bad practices in the selection of spatial or phylogenetic eigenvectors. Ecography, 41, 1–12

Bauman D., Fortin M-J, Drouet T. and Dray S. (2018b) Optimizing the choice of a spatial weighting matrix in eigenvector-based methods. Ecology

Bauman D., Vleminckx J., Hardy O., Drouet T. (2018c) Testing and interpreting the shared space-environment fraction in variation partitioning analyses of ecological data. Oikos

Blanchet G., Legendre P. and Borcard D. (2008) Forward selection of explanatory variables. Ecology, 89(9), 2623–2632

Legendre P., Gallagher E.D. (2001) Ecologically meaningful transformations for ordination of species data. Oecologia, 129(2), 271–280

Legendre P. and Legendre L. (2012) Numerical Ecology, Elsevier, Amsterdam

Peres-Neto P., Legendre P., Dray S., Borcard D. (2006) Variation partitioning of species data matrices: estimation and comparison of fractions. Ecology, 87(10), 2614–2625

Peres-Neto P. and Legendre P. (2010) Estimating and controlling for spatial structure in the study of ecological communities. Global Ecology and Biogeography, 19, 174–184

Author

David Bauman and Jason Vleminckx, davbauman@gmail.com, jasvlx86@gmail.com

Examples

# \donttest{
if(require(vegan)) { 
# Illustration of the test of the SSEF on the oribatid mite data
# (Borcard et al. 1992, 1994 for details on the dataset):
# Community data (response matrix):
data(mite)
# Hellinger-transformation of the community data (Legendre and Gallagher 2001):
Y <- decostand(mite, method = "hellinger")
# Environmental explanatory dataset:
data(mite.env)
# We only use two numerical explanatory variables:
env <- mite.env[, 1:2]
dim(Y)
dim(env)
# Coordinates of the 70 sites:
data(mite.xy)
coord <- mite.xy

### Building a list of candidate spatial weighting matrices (SWMs) for the 
### optimisation of the SWM selection, separately for 'Y' and 'env':
# We create five candidate SWMs: a connectivity matrix based on a Gabriel graphs, on
# a minimum spanning tree (i.e., two contrasted graph-based SWMs), either
# not weighted, or weighted by a linear function decreasing with the distance),
# and a distance-based SWM corresponding to the connectivity and weighting
# criteria of the original PCNM method:
candidates <- listw.candidates(coord, nb = c("gab", "mst", "pcnm"), weights = c("binary",
                                                                                "flin"))
### Optimisation of the selection of a SWM:
# SWM for 'Y' (based on the best forward-selected subset of MEM variables):
modsel.Y <- listw.select(Y, candidates, method = "FWD", MEM.autocor = "positive",
                         p.adjust = TRUE)
                         
names(candidates)[modsel.Y$best.id]                 # Best SWM selected
modsel.Y$candidates$Pvalue[modsel.Y$best.id]        # Adjusted p-value of the global model
modsel.Y$candidates$N.var[modsel.Y$best.id]         # Nb of forward-selected MEM variables
modsel.Y$candidates$R2Adj.select[modsel.Y$best.id]  # Adjusted R2 of the selected MEM var.

# SWM for 'env' (method = "global" for the optimisation, as all MEM variables are required
# to use MSR):
modsel.env <- listw.select(env, candidates, method = "global", MEM.autocor = "positive",
                           p.adjust = TRUE)

names(candidates)[modsel.env$best.id]                  # Best SWM selected
modsel.env$candidates$Pvalue[modsel.env$best.id]       # Adjusted p-value of the global model
modsel.env$candidates$N.var[modsel.env$best.id]        # Nb of forward-selected MEM variables
modsel.env$candidates$R2Adj.select[modsel.env$best.id] # Adjusted R2 of the selected MEM var.

### We perform the variation partitioning:
# Subset of selected MEM variables within the best SWM:
MEM.spe <- modsel.Y$best$MEM.select

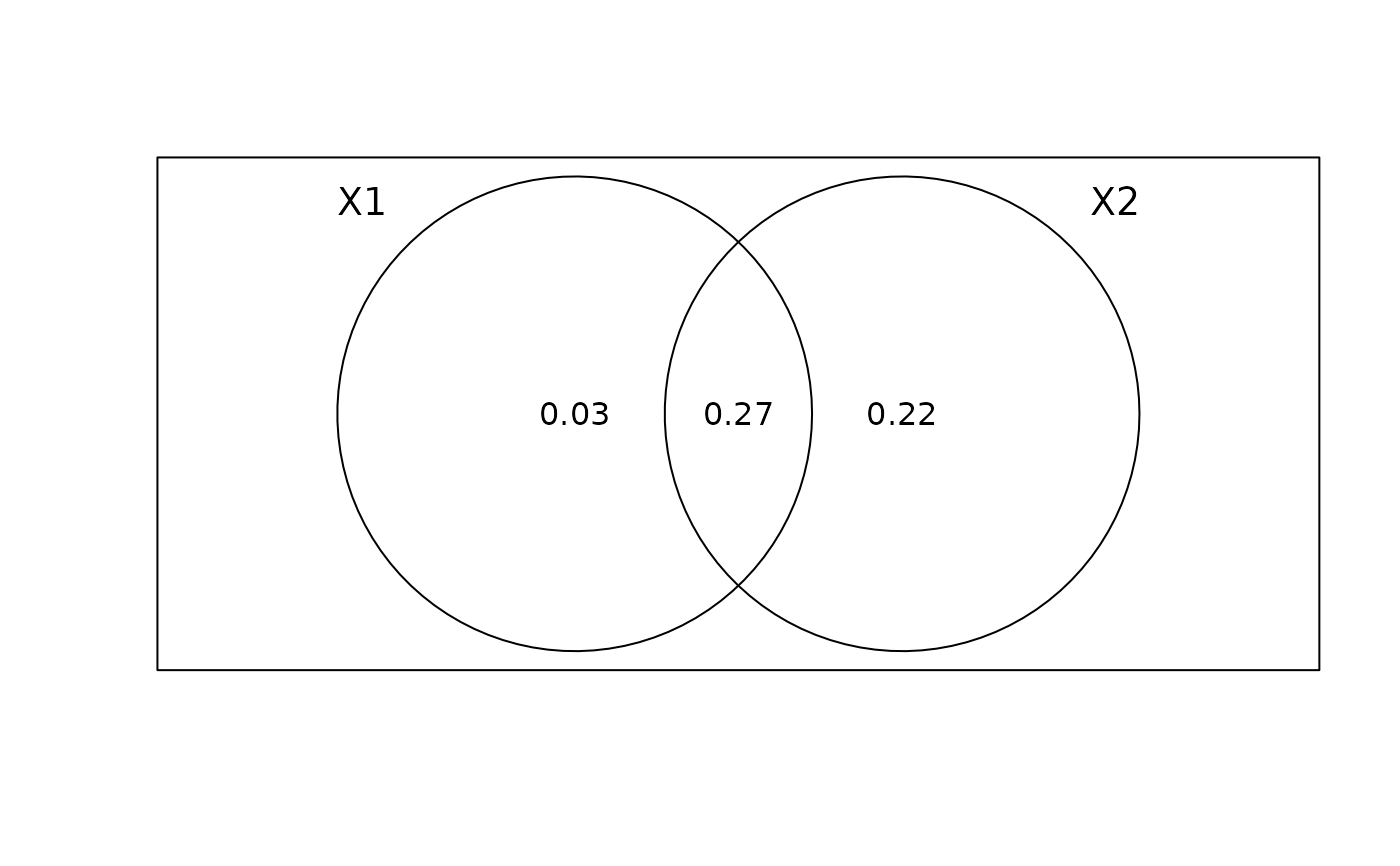
VP <- varpart(Y, env, MEM.spe)
plot(VP)

# Test of the shared space-environment fraction (fraction [b]):
SSEF.test <- envspace.test(Y, env, coord, MEM.spe, 
                           listw.env = candidates[[modsel.env$best.id]], 
                           regular = FALSE, nperm = 999)
SSEF.test

# The SSEF is highly significant, indicating a potential induced spatial dependence.
}
#> Warning: zero sum general weights
#> Procedure stopped (adjR2thresh criteria) adjR2cum = 0.452381 with 11 variables (> 0.446534)
#> Procedure stopped (alpha criteria): pvalue for variable 14 is 0.072000 (> 0.050000)
#> Procedure stopped (alpha criteria): pvalue for variable 14 is 0.098000 (> 0.050000)
#> Procedure stopped (alpha criteria): pvalue for variable 13 is 0.061000 (> 0.050000)
#> Procedure stopped (alpha criteria): pvalue for variable 12 is 0.061000 (> 0.050000)

#> Monte-Carlo test
#> Call: as.randtest(sim = E.b, obs = R2.b, alter = alternative)
#> 
#> Observation: 0.21545 
#> 
#> Based on 999 replicates
#> Simulated p-value: 1 
#> Alternative hypothesis: greater 
#> 
#>     Std.Obs Expectation    Variance 
#> -2.94921170  0.41168982  0.00442754 
# }