Combine dbMEM matrices corresponding to groups of sites

This function reads a file containing the Cartesian coordinates of sites forming different groups on the map, and constructs a combined staggered matrix of dbMEM spatial eigenvectors, ready for use in RDA. The method was first described and used in Declerck et al. (2011) and summarized in the Borcard et al. (2011) book, section 7.4.3.5. These publications provided preliminary versions of the present function. The present version is more completely documented. Furthermore, it uses the dbmem function of the adespatial package for computation of the eigenfunctions.

create.dbMEM.model(coord = NULL, D.mat = NULL, nsites)

Arguments

coord: Optional file containing the Cartesian coordinates of the sites.
D.mat: Optional distance matrix provided by user, class matrix or dist. If D.mat=NULL, the geographic distance matrix will be computed from the coordinates provided in file coord.
nsites: A vector containing the number of sites per group.

Value

A matrix with n rows containing a set of k staggered matrices of dbMEM eigenfunctions in its diagonal portion; n is the total number of sites in the study and k is the number of groups. Each small matrix contains the dbMEM functions, modelling positive spatial correlation, describing the spatial relationships among the sites of a group. The remainder of the matrix is filled with zeros. Zero is the mean value of all eigenfunctions describing within-group relationships. This means that during the calculation of RDA, the sites of a focus group will have, with each other, relationships described by the dbMEM eigenfunctions of that group, whereas the sites outside that group will have weights of 0 in the regressions that concern these eigenfunctions.

Details

The geographic positions of the sites are provided either in a file of geographic coordinates coord or as a geographic distance matrix D.mat.

The sites must, of course, be in the same order in file coord (or in file D.mat) and in the response data file used in the RDA. All sites of a group must be together in these two files, i.e. not interspersed. The numbers of sites in the groups are provided in vector nsites. See example.

File vector coord, if provided, must contain Cartesian coordinates of the sites, not coordinates in degrees. The Euclidean distance computed from the geographic coordinates is a meaningful representation of the geographic relationships only if the coordinates are Cartesian. Geodetic Cartesian coordinates can be derived from Lat-Lon data in degrees using the function geoXY of the SoDA package. Beware of UTM coordinates if the sites are not all located in the same UTM zone; UTM coordinates are Cartesian only within an UTM zone. See https://en.wikipedia.org/wiki/Universal_Transverse_Mercator_coordinate_system.

References

Borcard, D., F. Gillet and P. Legendre. 2011. Numerical ecology with R. Use R! series, Springer Science, New York.

Declerck, S. A. J., J. S. Coronel, P. Legendre & L. Brendonck. 2011. Scale dependency of processes structuring metacommunities of cladocerans in temporary pools of High-Andes wetlands. Ecography 34: 296-305.

Author

Pierre Legendre pierre.legendre@umontreal.ca, 2010. Adaptation to adespatial: Daniel Borcard and Pierre Legendre, 2016

Examples

{
 # Generate random coordinates for 35 sites forming 6 distinct groups on the map
 Easting <- runif(35)+c(rep(0,6),rep(1.5,7),rep(3,6), rep(0,5),rep(1.5,5),rep(3,6))
 Northing<- runif(35)+c(rep(2.8,6),rep(2.3,7),rep(2.8,6), rep(0,5),rep(0.5,5),rep(0,6))
 cartesian <- cbind(Easting,Northing)
 rownames(cartesian) <- paste("S",1:nrow(cartesian),sep='')
 nsites.per.group <- c(6,7,6,5,5,6)

 result <- create.dbMEM.model(coord=cartesian, nsites=nsites.per.group)

 # Draw a map to check the coding of the sites into the groups
 site.codes <- unlist(apply(cbind(1:6),1,n=nsites.per.group,function(a,n) rep(a,n[a])))

 col.vec <- c("green3","gray99","orange2","gold1","brown3","gray70")
 plot(cartesian, pch=22, col="black", bg=col.vec[site.codes], cex=2, ylim=c(0,4),asp=1)
 text(cartesian,labels=rownames(cartesian), cex=0.5, pos=3)

 # Examine the staggered matrix of dbMEM eigenfunctions
 # Not run:
 result
}

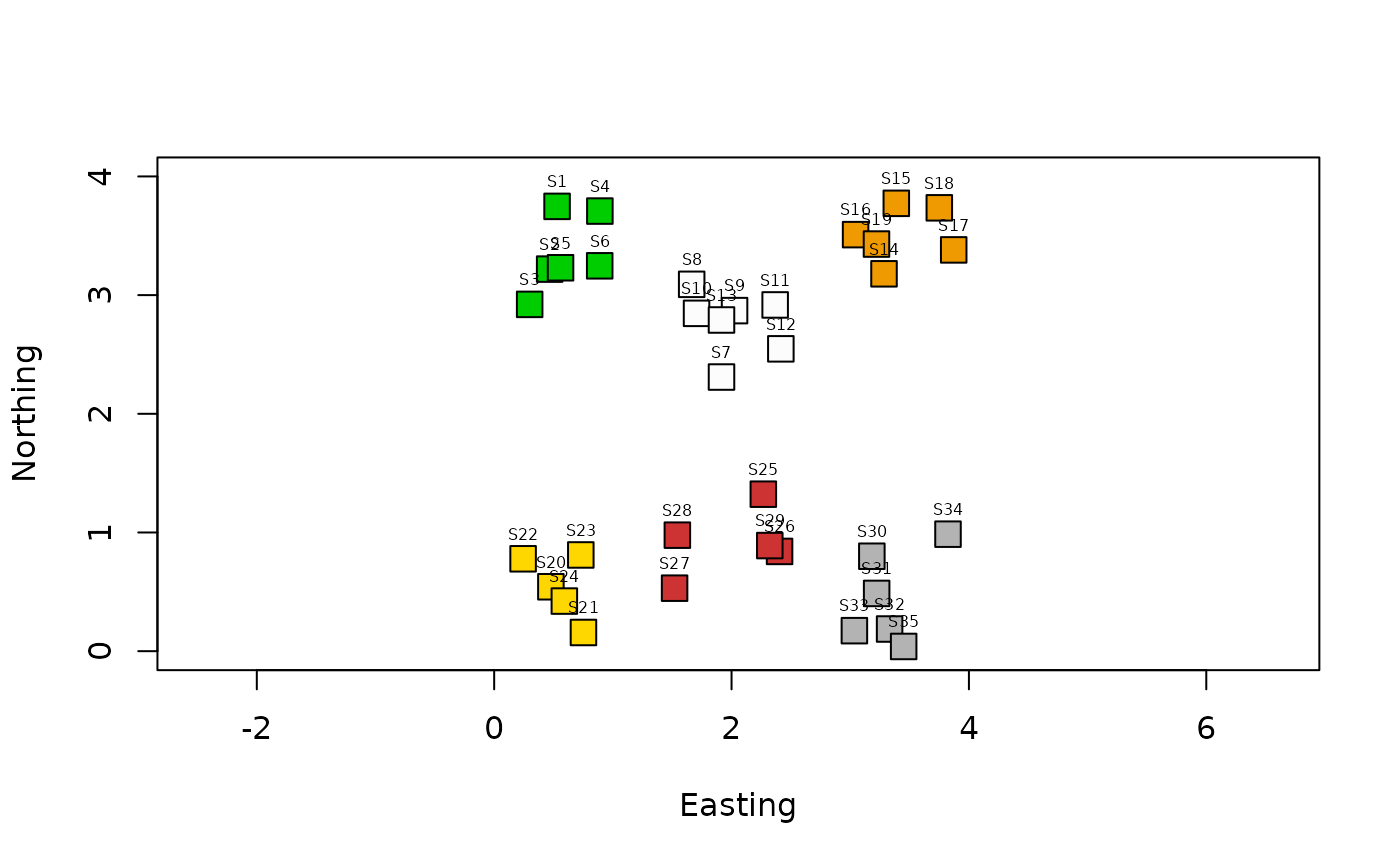#>         dbMEM.1    dbMEM.2    dbMEM.3    dbMEM.4    dbMEM.5    dbMEM.6
#> S1   1.32901379  1.0852980  0.0000000  0.0000000  0.0000000  0.0000000
#> S2  -0.90398444 -0.1517408  0.0000000  0.0000000  0.0000000  0.0000000
#> S3  -0.89910191  1.3310422  0.0000000  0.0000000  0.0000000  0.0000000
#> S4   1.34157518 -0.3794479  0.0000000  0.0000000  0.0000000  0.0000000
#> S5  -0.89853398 -0.1987509  0.0000000  0.0000000  0.0000000  0.0000000
#> S6   0.03103135 -1.6864007  0.0000000  0.0000000  0.0000000  0.0000000
#> S7   0.00000000  0.0000000  0.2873794  2.2130129  0.0000000  0.0000000
#> S8   0.00000000  0.0000000 -1.0772543 -0.3863427  0.0000000  0.0000000
#> S9   0.00000000  0.0000000 -0.5276669 -0.8426107  0.0000000  0.0000000
#> S10  0.00000000  0.0000000 -1.0881046 -0.3864892  0.0000000  0.0000000
#> S11  0.00000000  0.0000000  1.2018422 -0.6878058  0.0000000  0.0000000
#> S12  0.00000000  0.0000000  1.6328083 -0.5102193  0.0000000  0.0000000
#> S13  0.00000000  0.0000000 -0.4290042  0.6004547  0.0000000  0.0000000
#> S14  0.00000000  0.0000000  0.0000000  0.0000000 -0.8455539 -0.6359868
#> S15  0.00000000  0.0000000  0.0000000  0.0000000  0.2876765  1.8166640
#> S16  0.00000000  0.0000000  0.0000000  0.0000000 -0.8579841 -0.5939075
#> S17  0.00000000  0.0000000  0.0000000  0.0000000  1.2014985 -1.2987077
#> S18  0.00000000  0.0000000  0.0000000  0.0000000  1.3318386  0.3209196
#> S19  0.00000000  0.0000000  0.0000000  0.0000000 -1.1174755  0.3910184
#> S20  0.00000000  0.0000000  0.0000000  0.0000000  0.0000000  0.0000000
#> S21  0.00000000  0.0000000  0.0000000  0.0000000  0.0000000  0.0000000
#> S22  0.00000000  0.0000000  0.0000000  0.0000000  0.0000000  0.0000000
#> S23  0.00000000  0.0000000  0.0000000  0.0000000  0.0000000  0.0000000
#> S24  0.00000000  0.0000000  0.0000000  0.0000000  0.0000000  0.0000000
#> S25  0.00000000  0.0000000  0.0000000  0.0000000  0.0000000  0.0000000
#> S26  0.00000000  0.0000000  0.0000000  0.0000000  0.0000000  0.0000000
#> S27  0.00000000  0.0000000  0.0000000  0.0000000  0.0000000  0.0000000
#> S28  0.00000000  0.0000000  0.0000000  0.0000000  0.0000000  0.0000000
#> S29  0.00000000  0.0000000  0.0000000  0.0000000  0.0000000  0.0000000
#> S30  0.00000000  0.0000000  0.0000000  0.0000000  0.0000000  0.0000000
#> S31  0.00000000  0.0000000  0.0000000  0.0000000  0.0000000  0.0000000
#> S32  0.00000000  0.0000000  0.0000000  0.0000000  0.0000000  0.0000000
#> S33  0.00000000  0.0000000  0.0000000  0.0000000  0.0000000  0.0000000
#> S34  0.00000000  0.0000000  0.0000000  0.0000000  0.0000000  0.0000000
#> S35  0.00000000  0.0000000  0.0000000  0.0000000  0.0000000  0.0000000
#>        dbMEM.7       dbMEM.8    dbMEM.9   dbMEM.10
#> S1   0.0000000  0.0000000000  0.0000000  0.0000000
#> S2   0.0000000  0.0000000000  0.0000000  0.0000000
#> S3   0.0000000  0.0000000000  0.0000000  0.0000000
#> S4   0.0000000  0.0000000000  0.0000000  0.0000000
#> S5   0.0000000  0.0000000000  0.0000000  0.0000000
#> S6   0.0000000  0.0000000000  0.0000000  0.0000000
#> S7   0.0000000  0.0000000000  0.0000000  0.0000000
#> S8   0.0000000  0.0000000000  0.0000000  0.0000000
#> S9   0.0000000  0.0000000000  0.0000000  0.0000000
#> S10  0.0000000  0.0000000000  0.0000000  0.0000000
#> S11  0.0000000  0.0000000000  0.0000000  0.0000000
#> S12  0.0000000  0.0000000000  0.0000000  0.0000000
#> S13  0.0000000  0.0000000000  0.0000000  0.0000000
#> S14  0.0000000  0.0000000000  0.0000000  0.0000000
#> S15  0.0000000  0.0000000000  0.0000000  0.0000000
#> S16  0.0000000  0.0000000000  0.0000000  0.0000000
#> S17  0.0000000  0.0000000000  0.0000000  0.0000000
#> S18  0.0000000  0.0000000000  0.0000000  0.0000000
#> S19  0.0000000  0.0000000000  0.0000000  0.0000000
#> S20 -0.7336169  0.0101697203  0.0000000  0.0000000
#> S21  1.4279562 -0.0004680646  0.0000000  0.0000000
#> S22 -0.8513169  1.5712058475  0.0000000  0.0000000
#> S23 -0.8395760 -1.5909455616  0.0000000  0.0000000
#> S24  0.9965536  0.0100380584  0.0000000  0.0000000
#> S25  0.0000000  0.0000000000 -0.9613424  0.0000000
#> S26  0.0000000  0.0000000000 -0.9656062  0.0000000
#> S27  0.0000000  0.0000000000  1.3105440  0.0000000
#> S28  0.0000000  0.0000000000  1.0943074  0.0000000
#> S29  0.0000000  0.0000000000 -0.4779028  0.0000000
#> S30  0.0000000  0.0000000000  0.0000000  0.9088247
#> S31  0.0000000  0.0000000000  0.0000000 -0.5366064
#> S32  0.0000000  0.0000000000  0.0000000 -0.5752916
#> S33  0.0000000  0.0000000000  0.0000000 -0.5633614
#> S34  0.0000000  0.0000000000  0.0000000  1.7875043
#> S35  0.0000000  0.0000000000  0.0000000 -1.0210697